강력한 테일러 시리즈와 멱급수

INTRO

미적분학의 발전은 어떠한 형태의 함수라도 멱급수라는 연속된 변수들의 모임으로 정의가 가능함을 보였다. 이 멱급수는 함수를 S(x)라는 합의 형태로 대신한다. 이번 장에서는 우리에게 익숙한 기본 함수들의 멱급수 형태를 알아보고 그 정의를 배워보기로 하자.

삼각 함수와 멱급수

우리는 이미 삼각함수의 sin과 cos 그래프가 다음과 같은 형태로 반복된다는 것을 알고 있다.

 

사인과 코사인 함수의 형태

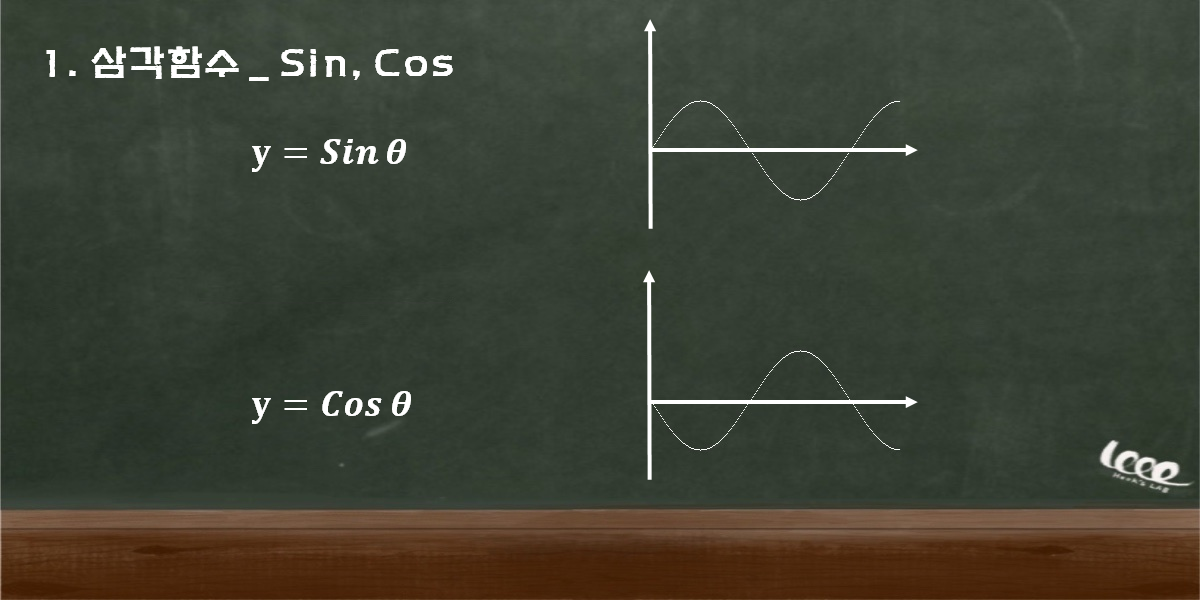
이 사인과 코사인이라는 함숫값을 변수로만 나타낼 수 없을까? 이에 대한 해답은 멱급수(power series)가 제공한다. 놀랍게도 사인과 코사인은 다음과 같은 시리즈로 나타내는 것이 가능하다.

 

사인 함수와 코사인 함수의 멱급수 전개식

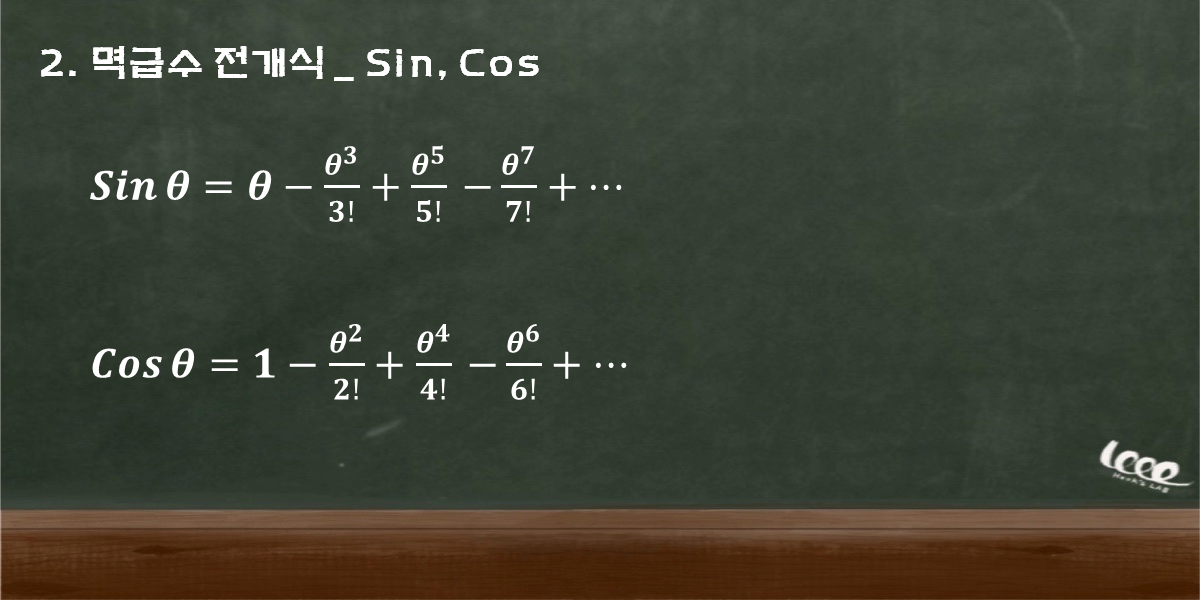
이처럼 변수가 지수(power)를 가지고, 급수(series) 형태로 구성된 함수를 멱급수(power series)라고 부른다. 그렇다면 어떻게 함수가 이러한 형태를 가진다는 것을 알아낼 수 있었는가?

멱급수 형태 유도 과정

어떤 함수가 멱급수로 전개 가능하다는 것을 유도하기 위해서 한 가지 가정이 필요하다. 바로 함수가 급수(series)라는 형태로 전개가 가능하다는 것이다.

 

먼저, 사인 함수가 다음과 같이 초기항과 변수의 거듭제곱 꼴이 상수라는 계수를 가진다고 가정해보기로 하자. (이것이 바로 멱급수의 일반항이다.) 그리고 계수를 결정하기 위해 x에 0을 대입하면 초기항을 알 수 있다. 

사인함수의 멱급수 유도과정

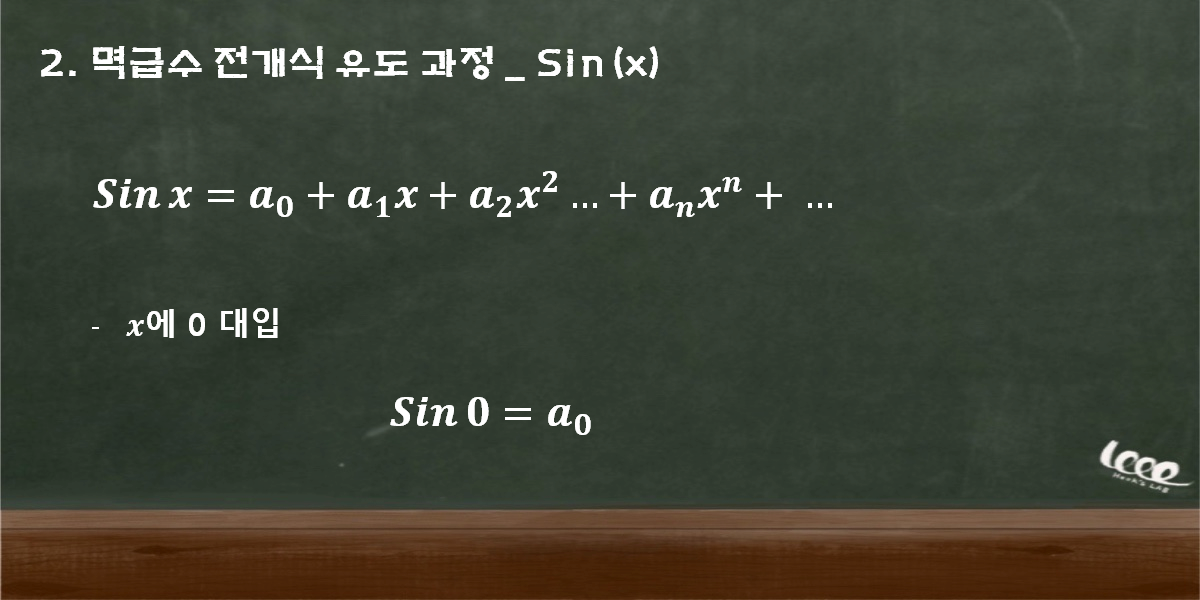
그리고 차례차례의 계수를 구하기 위해 우리는 미분을 활용할 것이다. 미분을 1회 시행해보자.

그리고 다시  x=0을 대입한다. 그러면 다음 항의 상수항이 결정된다.

 

사인함수의 멱급수 유도과정 2

 

위와 같이 미분과 (x=0) 대입을 2회, 3회, 반복해보면서 계수를 하나하나 보기로 하자.

 

사인함수의 멱급수 유도과정 3

 

미분을 3회까지 진행해본 결과, 우리는 n번째 계수가 다음과 같이 될 것을 추측할 수 있다.

 

사인함수의 멱급수 유도과정 4

 

이렇게 계수까지 결정된 멱급수의 총합이 수렴된다는 것을 결정하는 것을 수렴성 조사(test)라고 한다.

 

최종적으로 다음과 같이 사인과 코사인 함수의 멱급수 형태를 다음과 같이 정리한다.

 

사인함수와 코사인 함수의 멱급수

 

* 코사인 함수의 유도는 사인 함수의 유도 과정과 동일하다.  

 

다루지는 않았지만, 수렴을 전제로 다음과 같이 사인 함수의 멱급수 형태를 알게 되었다. 이렇게 미분을 이용해서 멱급수 형태를 알아내는 것을 원점(origin)에 대한 맥클로린 급수(Maclaurin series) 또는 테일러급수(Taylor series)라고 한다. 일반적으로 테일러급수의 경우 0 대신 a라는 상수를 갖는 (x-a)를 기본 지수로 대입하여 멱급수를 전개한다.  그리고 몇몇 다른 함수들은 이 방식이 멱급수를 알아내는데 용이하다.