π 이야기
우리가 어렸을 때 가장 먼저 접하게 되는 무리수는 아마도 파이, π 가 아닐까 하는 생각이 듭니다. 파이는 3.141592.... 을 나타내는 상수입니다. 반지름의 길이가 1인 원의 둘레는 3.141592.. 보다 두 배 크지요. 다시 말해서, 파이는 원둘레와 지름의 비를 나타내는 상수이며, 이 상수는 정말 편리한 개념입니다. 파이라는 단 하나의 정보가 2 개 이상의 정보를 내포하기 때문이죠. 비유하자면 1차원의 세계에서 다차원 세계로 가는 문 정도가 되겠네요.

그렇다면 파이는 언제부터 쓰였을까요? 기원전 1900년 경, 바빌로니아의 이집트 사람들이 최초로 이 원주율을 기록한 것이 남아있다고 하니 정말 오래된 수학 개념이라고 말할 수 있겠네요. 더 나아가 아르키메데스는 정구십육각형을 이용하여, 파이의 값은 'X와 Y 사이의 값'이라고 계산을 했다고 합니다. 이후 스위스의 수학자 윌리엄 존스가 처음으로 파이의 기호를 π로 사용하는 것을 제안했다고 하네요. 1949년에는 컴퓨터가 개발된 이후 최초로 이 파이의 값을 소수 아래 2037 자리까지 계산했다고 하는데요, 현재는 약 31조 자리까지 계산되었다고 하니, 정말 파이는 끝이 없는 수네요.
π 계산의 역사
가장 먼저 고대의 이집트에서는 직접 원형 바퀴를 굴려서 파이를 3.16으로 계산하였다고 합니다. 그리고...
1593년, 프랑스의 수학자 프랑수아 비에트라는 사람은 미지수를 문자로 대체하는 표기법을 소개한 최초의 수학자로 파이를 무한한 다각형의 확장을 원에 수렴한다는 개념에 착안해 파이를 다음과 같이 루트의 무한급수로 표현하여 계산하였습니다.
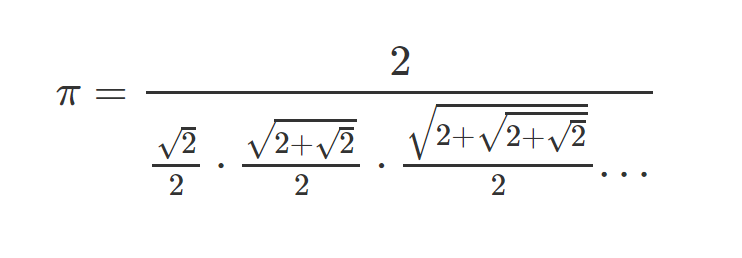
1655년, 무한대 기호와 파이를 무한곱으로 표현하는 수식을 만든 영국의 수학자 존 윌리스는 파이를 무한곱으로 나타내었습니다. 무한곱은 대문자 파이를 통해서 표현하고, 다음과 같이 파이를 계산했습니다.
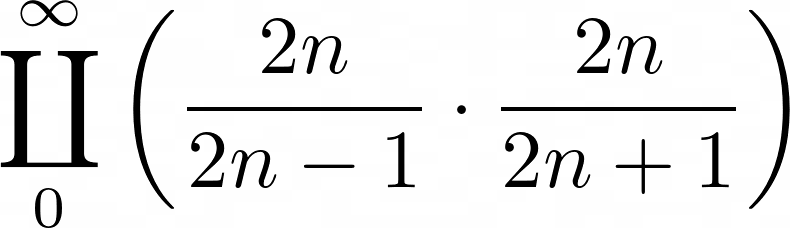
1671년, 수렴과 발산이라는 단어를 처음 사용한 제임스 그레고리가 아크 탄젠트의 급수를 발견하고, 그 식에 독일의 유명한 수학자 라이프니츠가 x=1을 대입하여, 파이를 4로 나눈 값을 급수 형태로 나타내었습니다.

1735년, 스위스의 위대한 수학자 오일러에 의해서, 자연수의 제곱을 역수로 하는 수들의 합에 의해서 원주율과 관계된 다음의 식이 나왔습니다.

언급한 계산방법 외에도 파이를 구하는 데에는 다양한 수학적 방법들이 존재합니다. 예를 들면, 다른 삼각함수를 통해서도 파이를 유도해 낼 수 도있겠으며, 가우스 적분식을 이용하여 파이를 구할 수 도 있습니다. 단순히 원둘레에서 시작한 파이 상수는 이처럼 여러 수학적 개념의 발전에 영향을 주었나 봅니다.
'RESEARCH > A piece of INFO.' 카테고리의 다른 글
| 알고리즘 표기법과 읽는 방법 (0) | 2022.03.04 |
|---|---|
| 단위에 중요한 접두사 용어 정리 (0) | 2021.12.15 |
| 화음에도 이름이 있다? (0) | 2021.12.06 |
| 다장조에도 조성 변화를 줄 수 있을까? (0) | 2021.11.29 |
| 연구실 안전 교육 (0) | 2021.06.02 |

